Uruguay vs. Portugal: Te Digo los Resultados de Octavos de Final
Por Augusto Souto*
Se viene Uruguay vs. Portugal y el Blog SUMA se la juega con un resultado exacto. En verdad no se la juega, analiza los resultados más probables en base a un modelo estadístico habitualmente utilizado para estos casos. A los amantes de las apuestas, una advertencia, el gran banco de inversiones Goldman Sachs incluyó a Arabia Saudita en octavos con un modelo bastante más complejo que el que comentaremos en esta nota, así que tomen sus precauciones.
En la simplicidad está la belleza, así que aquí les presentamos un modelo simple para predecir si Uruguay pasa a cuartos o no.
Predecir partidos de futbol es una tarea muy compleja dado que hay muchos factores que inciden en el resultado final. Por lo general para hacer estas predicciones apelamos a diferentes recursos como nuestro conocimiento de los equipos, nuestra intuición, el azar, etc. La estadística también puede ser un recurso valioso cuando queremos hacer una predicción de futbol de un partido, principalmente si en el mismo participan dos cuadros poco conocidos, la estadística, en función de los datos que tengamos y el modelo que construimos, nos puede dar un acercamiento a las diferentes probabilidades que tienen los posibles resultados del partido. Es por ello que diferentes instituciones como el banco de inversiones Goldman Sachs o el diario El País de Madrid construyen modelos sofisticados para calcular tales probabilidades.
Cabe aclarar que en cualquier modelo, las predicciones solo expresan una probabilidad, por lo que hasta en los modelos más sofisticados existirán errores de predicción (¿quién podría pronosticar el debacle alemán en fase de grupos?).
Generalmente, el mayor reto de este tipo de modelizaciones está en estimar la cantidad esperada de goles del equipo A y la cantidad esperada de goles del equipo B. La calidad de estas estimaciones dependerá especialmente de la cantidad de datos[1] con los que contemos y la habilidad que tengamos para definir como estos datos ayudan a inferir la cantidad de goles esperados.
A continuación presentamos los resultados de un modelo sencillo que hemos calibrado.
Tabla 1. Probabilidades de Ganar en Octavos de Final
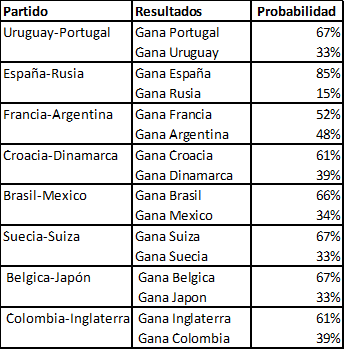
Tabla 2. Uruguay-Portugal: Probabilidad de resultados al final de los 90 minutos de juego

Tabla 3. Argentina-Francia: Probabilidad de resultados al final de los 90 minutos de juego
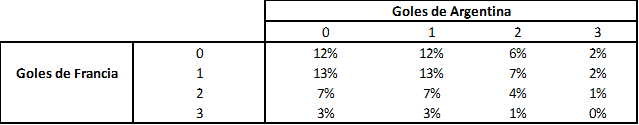
Como se puede observar en las probabilidades el modelo es bastante pesimista, nos dice que, la probabilidad de que gane Uruguay es de 33%, mientras que para Portugal es de 67%. Los resultados más probables en los 90 minutos de juego son: 1-0 Portugal (18% de probabilidad), los empates a 0 (14%) y a 1 (12%) y que gane Uruguay 1 a 0 (9%). Por supuesto, nada de esto tiene que ver con la fe que le tenemos a Uruguay en Blog SUMA, esto surge de datos históricos fríos.
Por otra parte, en el resto de los partidos de octavos de final, los equipos con mayor probabilidad de pasar de fase son España (85%), Suiza (67%), Brasil (66%), Croacia (61%) y Francia (52%).
Los resultados más probables en los 90 minuto de juego del partido Argentina-Francia son el empate a 1 (13% de probabilidad), una victoria 1-0 por parte de Francia (13%) y un 1-0 argentino (12%).
El método presentado es relativamente simple, por lo que no necesariamente podremos replicar las probabilidades que puede calcular una casa de apuestas. No obstante, en algunos de los partidos se observa cierta similitud entre los dividendos calculados mediante el método descrito y los ofrecidos por una casa de apuestas del mercado. Las discrepancias se deben principalmente a diferencias en los modelos (y los datos) utilizados así como a que dichas casas suelen ofrecer un dividendo menor al real para poder obtener una ganancia de la apuesta. Por lo tanto, siempre será muy difícil ganar dinero apostando incluso cuando tengamos modelos más sofisticados (salvo algunas excepciones). ¡Esperamos que se hayan divertido, y que apuesten a su propio riesgo, no nos hacemos responsables!
[1] Para hacer nuestras estimaciones, tomamos los partidos jugados por las selecciones mundialistas luego del mundial Brasil 2014.
* Investigador Asistente de CINVE. (Twitter: @AugustusSouto, email: [email protected]).
Anexo Metodológico
A continuación explicamos el modelo, cuyo único fin es recreativo.
Para modelar los resultados, una posible alternativa, es suponer (por simplicidad matemática) que los goles de los equipos son dos variables independientes (Maher, 1982). Bajo este supuesto, la probabilidad de que un partido entre el equipo A y el equipo B termine, por ejemplo, en un empate 1 a 1, sería el resultado del producto entre la probabilidad de que el equipo A haga un gol por la probabilidad de que el equipo B haga la misma cantidad de goles. Además, de modo de obtener cada una de esas dos probabilidades, es necesario asignar una distribución de probabilidad a la cantidad de goles que cada equipo hará. En general, este tipo de variables se llaman variables de conteo y se suelen modelar bajo una distribución de probabilidad llamada “Poisson”[1] y un parámetro ʎ que representa el valor esperado de la variable (en nuestra aplicación, la cantidad esperada de goles de un equipo).
Por simplicidad, propondremos una forma simple de estimar dichos parámetros. En primer lugar, requeriremos de una base de datos (que puede ser fácilmente copiada a una hoja de cálculo) con los resultados de los partidos jugados por ambos equipos. En segundo lugar, calcularemos la cantidad de goles anotados y recibidos en promedio[2] por cada uno de ellos (a los que llamaremos factores de fortaleza ofensiva y defensiva respectivamente). En tercer lugar, podemos tener una primera aproximación al parámetro ʎ del equipo A si multiplicamos el factor de fortaleza ofensiva del equipo A contra el factor de fortaleza defensiva del equipo B. De una manera similar, podemos establecer ʎ para el equipo B si usamos su fortaleza ofensiva y la fortaleza defensiva del equipo A. Sin embargo, debemos tener presente que la simplicidad de este método viene a costa de la precisión de nuestras estimaciones, dado que no todos los equipos han jugado con rivales similares (como si sucedería en una liga), ya que aquellos que juegan con equipos más vulnerables podrían tener más goles anotados y menos encajados en promedio.
Una manera relativamente sencilla de corregir este problema es incluyendo algún indicador de la jerarquía de los equipos en la fórmula de cálculo de los goles esperados. En este sentido, el ranking ELO[3] tiene la ventaja de indicar la jerarquía de los equipos (ya que los ordena como cualquier otro ranking) con el adicional de que este orden se construye mediante un sistema de puntos que son asignados a los países en función de la jerarquía del rival vencido así como de cuan abultado fue el resultado. Una estimación posible[4] del parámetro ʎ entonces podría ser la multiplicación de la fortaleza ofensiva del equipo por la fortaleza defensiva de su rival por un cociente entre los puntos ELO del equipo y los del rival:
Finalmente, una vez que se estiman los parámetros, a través de una planilla de cálculo podemos calcular la probabilidad de que cada equipo anote una cantidad concreta de goles (en Excel mediante la función Poisson).
Ejemplo: Uruguay vs Portugal
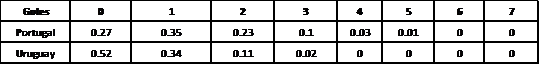
Luego, dado que asumimos que los goles de ambos equipos son independientes, la probabilidad de un resultado resulta de multiplicar la probabilidad de goles de cada equipo. En base a la multiplicación de las probabilidades de gol para cada equipo, se obtiene una la matriz de resultados presentada al principio de la nota.
En caso de empate, se supone que ambos equipos juegan un alargue donde cada ʎ ahora es igual al parámetro de tiempo reglamentario dividido por 3 ya que el anterior indicaba una probabilidad de ocurrencia durante 90 minutos y el nuevo parámetro define una probabilidad sobre 30 minutos de juego. Por último, la probabilidad de que ambos equipos terminen empatados en la prorroga se multiplica por 0.5 y se le asigna una probabilidad de victoria idéntica a cada equipo para determinar la chance de ganar por penales.
Finalmente, cabe mencionar que, el autor está abierto a cualquier corrección o sugerencia.
[1] En honor al matemático francés Denis Poisson. Ver detalles técnicos en https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson.
[2] En nuestro caso, para cada equipo, estas cantidades se normalizaron por la cantidad de goles que anotaron los equipos participantes de la misma confederación. De tal manera se logra capturar parcialmente el efecto de jugar en una confederación sobre los goles promedio ya que la mayoría de los partidos se juegan entre equipos de una misma confederación.
[3] Ver: https://es.wikipedia.org/wiki/Clasificaci%C3%B3n_Elo_del_f%C3%BAtbol_mundial
[4] Existen otras maneras de ajustar por el ranking. Idealmente, si se contara con una base de datos de partidos con el ranking de cada equipo y los goles, mediante un análisis de regresión se puede estimar un parámetro que indique el aumento esperado en los goles por cada punto en el ranking. Nuestra base aún no incorpora tales datos.
Muy interesante análisis.
Los supuestos parecen razonables. Más allá de que a priori pueda resultar demasiado forzado el supuestos de independencia entre los goles de uno y otro equipo y de distribución Poisson de los goles de cada equipo, en definitiva no influyen mayormente en la probabilidad de clasificarse de cada equipo. Incluso la forma utilizada para el cálculo de la tasa de Posisson resulta sensata.
Sin embargo, a partir de la información compartida en la ficha técnica, el modelo parece no estar considerando factores más difíciles de medir, como la localía, la fuerza que adquieren algunos equipos en instancias decisivas y cómo llegan hoy (rodaje, cansancio, lesiones, etc.).
Esto último se puede paliar ponderando más fuertemente en la tasa de Poisson los partidos más recientes, sobre todo los de este mundial. La localía de Rusia también puede compensarse asignándole un plus (el ranking ELO creo que la considera). Lo del temple de cada equipo es más difícil, pero se puede intentar ponderar más fuertemente a los partidos más importantes/decisivos (en la ficha técnica no queda claro cómo se consideró esto en el historial de partidos).
Estuve comparando las probabilidades de clasificar calculadas con las que surgen de los dividendos de las casas de apuestas (una vez descontada la comisión) y he podido apreciar que en casi todos los casos éstas le asignan más probabilidad al equipo que llega mejor, considerando el factor de localía de Rusia. Además, afortunadamente para nosotros, el peso de la camiseta celeste parece también estar influyendo positivamente en nuestras probabilidad de clasificar a cuartos de final.
País / Prob.SUMA / Prob.dividendos
Uruguay 33% 51%
Portugal 67% 49%
España 85% 76%
Rusia 15% 24%
Francia 52% 57%
Argentina 48% 43%
Croacia 61% 69%
Dinamarca 39% 31%
Brasil 66% 77%
México 34% 23%
Suecia 33% 47%
Suiza 67% 53%
Bélgica 67% 81%
Japón 33% 19%
Colombia 39% 39%
Inglaterra 61% 61%
Un saludo Diego, sería bueno que pusieras marcadores finales de los demás partidos.
Gracias x tu comentario!
Buena idea. Pero necesitamos esponsores xa generar mas resultados! Gracias x tu comentario!
Si bien los partidos de octavos de final son pocos como para poder sacar conclusiones definitivas, los resultados de los mismos se correspondieron en general con lo que más arriba sugería ajustarle al modelo: una influencia positiva en la probabilidad de superar la llave para el local (Rusia), para los equipos con mayor tradición (p,ej. Uruguay sobre Portugal) y para los que llegaron mejor al partido (p.ej. superaron la llave 6 primeros en su grupo y tan sólo 2 segundos).
Yendo a los números, el modelo SUMA acertó el clasificado en 5 de las 8 llaves (62,5%) mientras que el modelo en base a dividendos acertó 6 (75%). Hilando más fino, si se toma como error la distancia en valor absoluto entre las probabilidades estimadas (a priori) y lo que realmente ocurrió (probabilidad a posteriori 1 si ocurrió y 0 si no), el promedio de error para el modelo SUMA fue 0,52 mientras que el del modelo en base a dividendos fue de 0,42. Si en cambio hubiésemos aplicado un modelo donde la predicción se hubiera hecho simplemente asignando 50% de probabilidad a todos los equipos, el error obviamente hubiese sido 0,5 (estos errores se reducen a 0,38, 0,30 y 0,31 respectivamente para los tres modelos si no hubiésemos considerado los penales y por lo tanto en caso de empate al final del alargue hubiéramos asignado como probabilidad a posteriori 0,5 a ambos equipos).
Utilizando el modelo SUMA pero ajustando algo de lo que sugería más arriba, p.ej. simplemente sumando 20% por localía y 10% por haber sido primero de grupo (obviamente se puede intentar aplicar algo más refinado) se hubiera obtenido un error promedio de 0,44 (0,31 en caso de considerar empates antes de penales), bastante más bajo que el error del modelo SUMA original pero tampoco mucho mejor que el modelo al azar. Este tipo de consideraciones ya están incluidas en el modelo en base a dividendos y entiendo que en gran parte por eso es el modelo que ajustó mejor.
Sea como sea, a partir de mañana veremos qué ocurre con los cuartos de final.